My Currrent Research
My research lies at the interface of continuous optimization, (algorithmic) real algeraic geometry, computational topology. Nevertheless, any topic related to topology (Morse theory), geometry, and complexity of algebraic varieties (singularity theory, cohomology, and sheaf-theoretic algebraic geometry) and semi-algebraic sets and their applications to optimization and complexity fascinates me and captures my attention. My current research illuminates the role of topological invariants, algebraic degree, and singularity in computational complexity of semidefinite and polynomial optimization.
Degree and Convergence Rate of the Central Path
We studied the complexity of semidefinite optimization and central path (the red path in the 3-elliptope below) under the failure of the strict complementarity condition, which imposes further complications to the convergence of IPMs: 1) There is no Lipschitzian bound on the distance of central solutions to the limit point; 2) Central path is not analytic at the limit point (which results in a tangential convergence, as illustrated below). We developed a symbolic algorithm to compute real univariate representations describing the central path and its limit point, where the limit point is described by taking the limit of central solutions, as bounded points in the field of algebraic Puiseux series. We proved an upper bound on the degree of the Zariski closure of the central path and a lower bound on the convergence rate of the central path.
Complexity of Analyticity of the Central Path
It is well-known that the central path of semi-definite optimization, unlike linear optimization, has no analytic extension to the limit point in the absence of the strict complementarity condition. In essence, the superlinear convergence of
primal-dual IPMs rests on the analyticity of the central path at the limit point, which holds if and only if the strict complementarity condition holds. If the strict complementarity condition fails, the ramification index of the central path is strictly greater than 1 (e.g., the red branch at (0,-1) contains the graph of the central path in the picture below). We proposed a symbolic algorithm, based on real univariate representation of the central path and the Newton-Puiseux algorithm, with singly exponential complexity (in terms of the matrix size and the number of affine constraints) to compute a reparametrization that recovers the analyticity of the central path at the limit point.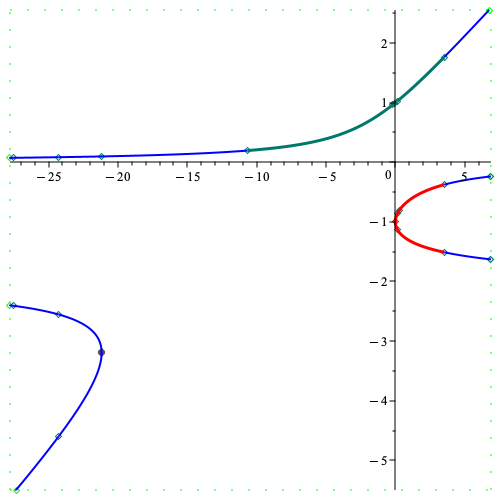
Improved Lojasiewicz Inequality in the Semi-Algebraic Category and Error Bounds in Optimization
Very recently, we proved a nearly tight upper bound on the Lojasiewicz exponent for semi-algebraic functions over a real closed field R in a very general setting. Unlike the previous best known bound in this setting due to Solerno, our bound is independent of the cardinalities of the semi-algebraic descriptions of f, g, and A. We exploited this fact to improve the best known error bounds for polynomial and non-linear semi-definite systems. As a result, we improved the best current error bound for polynomial and nonlinear semidefinite systems. As an abstraction of the notion of independence from the combinatorial parameters, we proved a version of Lojasiewicz inequality in polynomially bounded o-minimal structures. We proved existence of a common Lojasiewicz exponent for certain combinatorially defined infinite (but not necessarily definable) families of pairs of functions, which improves a prior result due to Chris Miller.
PhD Research
My past reserarch has substantial overlap with computational optimization, sensitivity analysis, and their applications. In my PhD, I developed a polynomial time Dikin-type affine scaling algorithm for symmetric conic optimization, which is a generalization of linear optimization, semidefinite and second-order conic optimization. I developed a methodology to approximate the optimal partition of semidefinite optimization, a concept which has its origin in linear optimization, and measure its complexity. Further, I used the theoretical developments for the optimal partition to either generate an approximate solution for semidefinite optimization or to speed up the convergence rate of interior point methods to the unique optimal solution of second-order conic optimization problems. I also studied the parametric analysis of semidefinite and second-order conic optimization problems using an optimal partition approach, where the objective function is perturbed along a fixed direction.
PhD Thesis: Conic Optimization: Optimal Partition, Parametric, and Stability Analysis. [PDF]
In Preparation
- Basu S, Mohammad-Nezhad A.O-minimal structures and critical paths in nonlinear optimization
- Basu S, Mohammad-Nezhad A.Morse inequalities on semi-algebraic sets and applications
- Basu S, Mohammad-Nezhad A., Sampourmahani, P., Terlaky, T. A superlinearly convergent interior point method for semi-definite optimization
Published
- Basu S, Mohammad-Nezhad A. Improved effective Lojasiewicz inequality and applications. To appear in Forum of Mathematics, Sigma (2024) [ArXiv]
- Basu S, Mohammad-Nezhad A. On the complexity of analyticity in semidefinite optimization. Advances in Applied Mathematics (2024) 156:102670. [ArXiv][Journal]
- Basu S, Mohammad-Nezhad A. On the central path of semidefinite optimization: degree and convergence rate. SIAM Journal on Applied Algebra and Geometry (2022) 6:299-318. [ArXiv][Journal]
- Hauenstein J., Mohammad-Nezhad A., Tang T., Terlaky, T. On computing the nonlinearity interval in parametric semidefinite optimization. Mathematics of Operations Research (2022) 47(4):2989-3009. [ArXiv][Journal]
- Mohammad-Nezhad A., Terlaky T. On the sensitivity of the optimal partition for parametric second-order conic optimization.Mathematical Programming B (2021) 189:491-525. [ArXiv][Journal]
- He S., Hwang J., Martins J., Shahabsafa M., Mohammad-Nezhad A., Lei W., Zuluaga L., Terlaky T. Mixed-integer Second-order Cone Optimization for Composite Discrete Ply-angle and Thickness Topology Optimization Problems. Optimization and Engineering (2021) 22:1589-1624. [Journal]
- Mohammad-Nezhad A., Terlaky T. Parametric analysis of semidefinite optimization. Optimization (2020) 69(1):187-216. [ArXiv] [Journal]
- Mohammad-Nezhad A., Terlaky T. Quadratic convergence to the optimal solution of second-order conic optimization without strict complementarity. Optimization Methods and Software (2019) 34(5):96-990. [Optimization-Online][Journal]
- Mohammad-Nezhad A., Terlaky T. On the identification of optimal partition for semidefinite optimization. INFOR: Information Systems and Operational Research (2019) 58(2):225-263. [Journal]
- Mohammad-Nezhad A., Terlaky T. A rounding procedure for semidefinite optimization. Operations Research Letters (2019) 47:59-65. [Journal]
- Shahabsafa M., Mohammad-Nezhad A., Terlaky T., Zuluaga L., He S., Hwang J., Martins J. A novel approach to discrete truss design problems using mixed integer neighborhood search.Structural and Multidisciplinary Optimization (2018) 58:2411-2429. [Journal]
- Mohammad-Nezhad A., Terlaky T. A polynomial primal-dual affine scaling algorithm for symmetric conic optimization. Computational Optimization and Applications (2017) 66:577-600. [Journal]
- Mohammad Nezhad A., Mahlooji H. An artificial neural network meta-model for constrained simulation optimization. Journal of the Operational Research Society (2014) 65(8):1232-1244. [Journal]
- Mohammad Nezhad A., Manzour H, Salhi S. Lagrangian relaxation heuristics for the uncapacitated single-source multi-productfacility location problem. International Journal of Production Economics (2013) 145(2):714-24. [Journal]
- Mohammad Nezhad A., Aliakbari Shandiz R, Eshraghniaye Jahromi A H. A particle swarm-BFGS algorithm for nonlinear programming problems. Computers and Operations Research (2013) 40(4):963-72. [Journal]
- Mohammad Nezhad A., Mahlooji H. A revised particle swarm optimization based discrete Lagrange multipliers method for nonlinear programming problems. Computers and Operations Research (2011) 38(8):1164-1174. [Journal]